
❓ 트리(Tree)란?
트리(Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다.
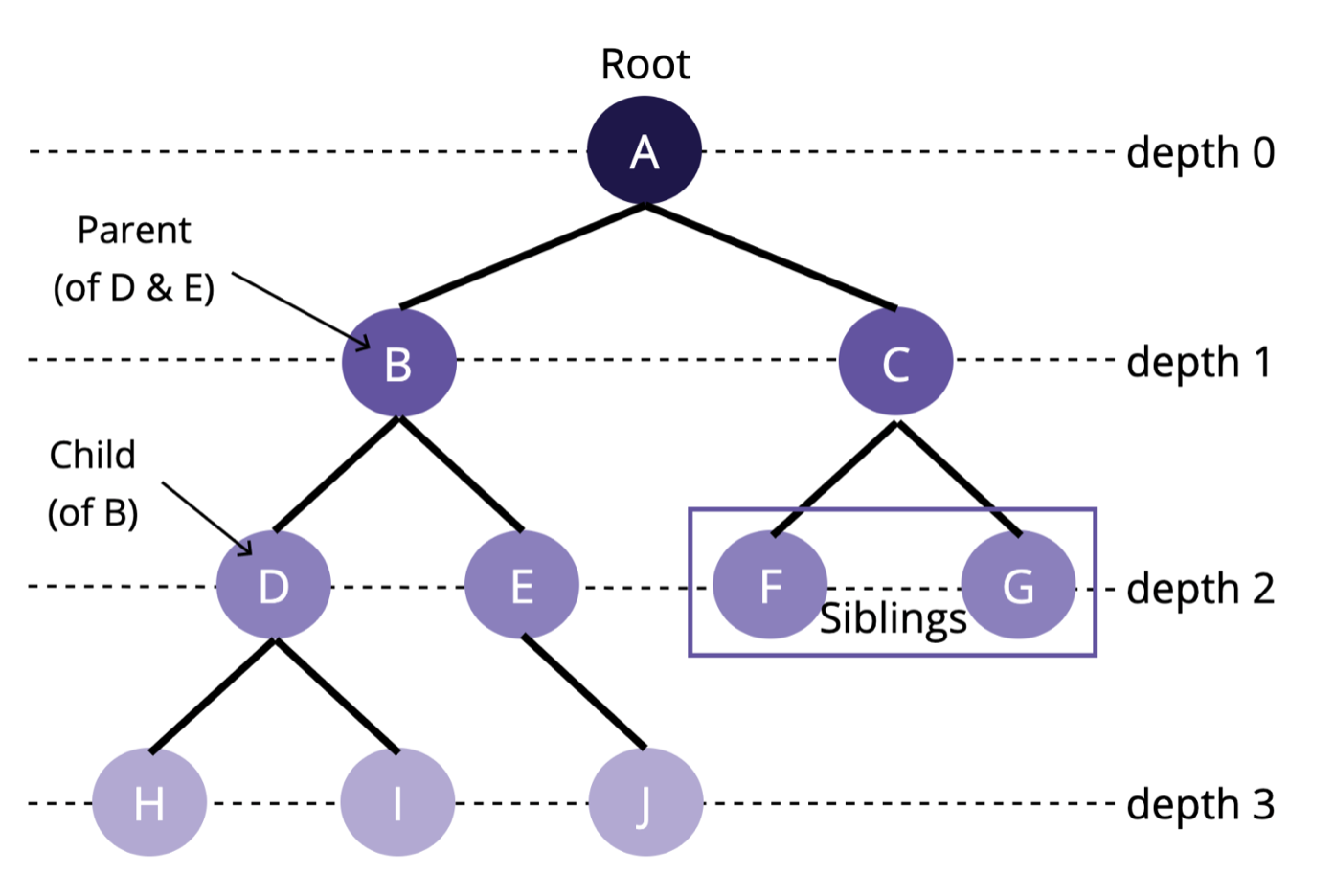
트리는 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다.
또한 트리 내에 다른 하위 트리가 있고, 그 하위 트리 안에는 또 다른 하위 트리가 있는 재귀적 자료구조이기도 합니다.
트리의 대표적인 예시로는 컴퓨터의 directory구조가 있습니다.
📌 트리 구조에서 사용되는 기본 용어
| 명칭 | 설명 |
| 노드(node) |
트리에서 데이터를 저장하는 기본적인 단위 그래프의 정점 |
| 루트 노드(root node) | 부모가 없는 노드, 트리 구조에서 최상위에 존재하는 A와 같은 노드 |
| 내부 노드(internal node) | 단말 노드가 아닌 노드 |
| 단말 노드(leaf node) | 자식이 없는 노드, (말단 노드, 잎 노드 라고도 부름) 밑으로는 또 다른 노드가 연결되어 있지 않은 H,I,J,F,G와 같은 노드 |
| 경로(edge) | 노드와 노드를 연결하는 연결선(link, branch 라고도 부름) 그래프의 간선 |
| 형제(sibling) | 같은 부모를 가지는 노드 |
| 노드의 크기(size) | 자신을 포함한 모든 자손 노드의 개수 |
| 노드의 깊이(depth) | 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수 루트 노드로부터의 거리 |
| 노드의 레벨(level) | 트리의 특정 깊이를 가지는 노드의 집합 |
| 노드의 차수(degree) | 하위 트리 개수 / 간선 수(degree) = 각 노드가 지닌 가지의 수 |
| 트리의 차수(degree of tree) | 트리의 최대 차수 |
| 트리의 높이(height) | 루트 노드에서 가장 깊숙히 있는 노드의 깊이 |
| 보조트리(Sub-Tree) | 큰 트리(전체)에서 속하는 작은 트리 트리 내의 하위집합 또는 부분집합 |
📌 트리의 특징
위에서 말했듯 그래프(Graph)는 정점(vertex)들과 간선(edge)들로 이루어진 추상적인 자료구조로, 그 중에서도 트리는 특별한 형태의 그래프입니다. 트리(Tree)는 아래와 같은 특징을 가지며, 이 특징들 때문에 그래프와는 다른 새로운 성질을 가지게 됩니다.
- 트리는 사이클(cycle)이 없는 비순환 구조
▪ 즉, 한 정점에서 출발하여 다시 자기 자신으로 돌아오는 경로가 존재하지 않습니다. - 하나의 루트 노드와 0개 이상의 하위 트리
▪ 루트 노드는 반드시 하나여야 하며, 두개가 될 수 없습니다 - 모든 노드는 단 하나의 부모(parent) 노드를 가짐
▪ 루트 노드를 제외한 모든 노드는 반드시 하나의 부모 노드를 가져야 합니다. - 노드가 N개인 트리는 항상 N-1개의 간선(edge)을 가짐
▪ 루트 노드를 제외한 모든 노드는 반드시 하나의 부모 노드를 가져야 합니다. - 모든 노드로 갈 수 있는 경로는 루트 노드를 거쳐야만 가능
▪ 다른 노드들이 모든 경로를 지나기 위해서는 반드시 루트 노드를 거치는 구조를 가집니다.
위와 같은 특징들로 트리(Tree)는 일반적인 그래프(Graph)와는 달리, 계층 구조(hierarchical structure)를 가지며, 데이터를 표현하거나 분석하기에 적합한 자료구조가 됩니다.
📌 트리의 종류
트리의 종류는 노드의 갯수나 위치에 따라서 결정됩니다.
✅ 이진트리(Binary Tree)
이진트리란 자식의 노드의 갯수가 두개 이하인 트리를 말합니다.
💠이진트리의 분류

- 정 이진 트리(full binary tree)
: 자식 노드가 0 또는 2개인 이진 트리 - 완전 이진 트리(complete binary tree)
: 왼쪽에서부터 채워져 있는 이진 트리
(마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있는 트리) - 변질 이진 트리(degenerate binary tree)
: 자식 노드가 하나밖에 없는 이진 트리 - 포화 이진 트리(perfect binary tree)
: 모든 노드가 꽉 차 있는 이진 트리. 반드시 노드의 개수가 2^(h+1)-1 의 개수를 가진다. (h=높이) - 균형 이진 트리(balanced binary tree)
: 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리
✅ 이진탐색트리(Binary Search Tree)
탐색을 위한 이진 트리의 일종으로 특수한 노드 값을 가지는 형태의 이진 트리입니다.
이진 탐색 트리에서 노드의 값이 저장되는 구조는 이렇습니다.
- left node에는 부모노드보다 작은 값이 저장됩니다.
- right node에는 부모노드보다 큰 값이 저장됩니다.
- 모든 노드는 중복된 값을 가지지 않습니다.

- 일반적인 비선형적인 구조로 잘 만들어진 이진 탐색 트리는 O(log n)의 시간복잡도를 가집니다.
그러나 이진 탐색트리는 데이터의 삽입 순서에 따라서 선형적인 구조를 가지게 될 수도 있어 시간복잡도가 변경되고, 최악읜 경우 O(n)의 시간복잡도를 가지게 될 수도 있습니다.
(여기서 트리는 일반적으로 비선형 구조, 하지만 이진트리에서는 특이케이스로 선형적인 구조를 가질 수도 있음)
✅ AVL트리
AVL트리는 이진 탐색 트리의 일종으로 이진 탐색 트리에 균형잡힌 트리를 유지하는 자료 구조입니다.
이진 탐색 트리와 같은 특징을 지니고 있지만, AVL트리는 균형 트리의 특징을 가져 서브트리의 좌, 우 높이가 1(-1, 0, 1)을 초과하지 않도록 동작합니다.

만약 AVL트리에서 균형이 무너지게 된다면, 새로운 노드를 추가하거나 왼쪽이나 오른쪽으로 돌리는 회전을 통해 균형을 유지합니다.
균형을 잃은 상황(예시)
A
\
B
\
C
\
D
균형을 맞춘 결과(예시)
B
/ \
A C
/ \
D (E)
- 이런 방식으로 AVL트리는 항상 균형을 맞춰 높이를 유지하기 때문에 평균이든 최악이든 시간복잡도는 O(log n)을 가지게 됩니다.
✅ 그 외 트리들
- 트라이(Trie)
- 스플레이 트리(Splay tree)
.Reference
트리(Tree)에 대해서 알아보자
이전 포스팅 그래프(Graph)에 이어서 이번엔 트리(Tree)에 대해서 알아보자 트리(Tree)란? 트리는 그래프의 하위 개념 중 하나이다. 트리를 그래프의 특징에 따라서 정의하게 된다면. > 트리는 방향성
velog.io
'프론트엔드 면접 질문 > 자료구조와 알고리즘' 카테고리의 다른 글
| [자료구조] 그래프(Graph)의 탐색 및 구현 (0) | 2024.03.29 |
|---|---|
| [자료구조] 그래프(Graph)의 개념 (0) | 2024.03.29 |
| [자료구조] 스택(Stack)과 큐(Queue) (0) | 2024.03.27 |
| [자료구조] 자료구조의 종류와 분류 (0) | 2024.03.27 |
| [자료구조] 자료구조란 (0) | 2024.03.27 |



